迪士尼彩乐园ll 【分形】一根线, 能折叠出系数这个词寰宇吗?
发布日期:2024-12-06 12:34 点击次数:152
用一根一维的线能折叠出系数这个词寰宇吗?谜底是:也不是彻底莫得可能迪士尼彩乐园ll。
1890年,数学家皮亚诺闲来无事搞出了这么一种线。他先将一个大正方形九等分,再用一条线相连系数小正方形的中心点,取得一个Z型弧线。然后再把每个小正方形九等分,再相连系数小正方形中心点,依此类推,直至无限。此时的它就酿成了一个二维的面,这就是着名的皮亚诺弧线。


一年后,大数学家希尔伯特在此基础上也忽视了一种线。他将正方形4等分后相连中心点,取得一个U型弧线。然后再对每个小正方形作念相通操作,直至无限。这就是希尔伯特弧线。希尔伯特弧线比皮亚诺弧线轨则性更强。但它们的存在引出了一个重大问题:为什么一维的线一会儿就能酿成二维的面?于是东谈主们迟缓清楚到,在通例的整数维之间应该还存在着一种非整数维,分形学的种子就此萌生。
1904年,数学家科赫也忽视了一种弧线。他将一段线段三等分,然后在中间的线段处向外隆起一个三角形。终末再对新图案的每一条边作念相通操作,直至无限。这就是着名的科赫弧线。

科赫弧线完满体现了分形结构的中枢特色:自相似性,即不管放大或者减弱几许倍,总能看到探究或类似的结构。天然界存在着大齐的分形结构,比如一派雪花,放大之后还能看到更小的雪花。树杈的树杈上还有更小的树杈,套娃底下是更小的套娃。
这种结构的神奇之处在于,从中取下淘气一个局部齐包含了合座的系数信息,以至于有不少东谈主将其视为万物的终极密码。另外由于每次分形齐将本来的总线段长度增多了4/3倍,这意味着当分形次数达到无限,这个有限面积下的图案就能领有无限大的边长。
而更神奇的是,数学家商量出科赫弧线的维度并非是单纯的一维或者二维,而是1.26维。咱们常说的维度齐是拓扑维度,它默示细则空间中一个点所需要的变量数,比如三维空间的一个点需要三个变量方能唯独细则。同理如果一个空间中的点只需两个变量就能细则,那它就是二维的面。地球名义近似为一个二维曲面,因为只需要经度和纬度就能考究则位你的位置。而四维空间的点就需要四个变量才能态状。

天然三维空间的咱们无法思象,但数学上并无结尾。按照拓扑维数的界说,一条线不管多长多复杂齐应该是一维。但目下皮亚诺和希尔伯特弧线既然填满了系数这个词正方形,那它们就应该是二维。于是矛盾出现,拓扑学独创东谈主豪斯多夫坐窝清楚到既然传统拓扑学的维数商量形势照旧无法搞定,这种空间上无限的复杂度就需要一种全新的维度商量形势。
当咱们把一条线段两等分时不错取得两条线段,把一个正方形的边两等分就不错取得四个小正方形,把一个立方体的边两等分不错取得八个小立方体。于是豪斯多夫将其执行,如果把一个东西的边分红R等份后取得了N个小东西,这个指数D就是该物体的维度。反过来取对数,于是咱们就取得了淘气物体的维度商量形势。
根据科赫弧线的性质,咱们可按其基本长度的1/3来进行分段,分段后是4条更小的科赫弧线,于是就取得了科赫弧线的维数约等于1.26,这就是分形额外的数学性质。科赫弧线明明仅仅一条线,但因为它是一条领有无限细节的线,导致它不再是一维而是1.26维。这意味着分形不错为物体增多一个突出维度,出现分数维。

天然分形也并不全是分数维,比如当咱们将科赫弧线中三角形的夹角不绝减弱,其分形维度就会迟缓增多。而当中间彻底酿成一段隆起的线段后,它就铺满了这个鸿沟内的系数这个词平面,对应的维度就酿成2,此时的它已不再是线而是成为了一系数这个词面。
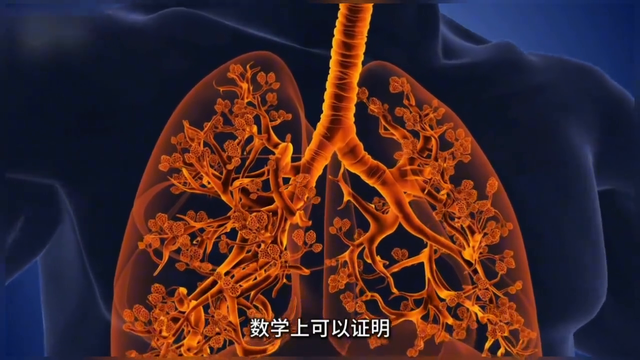
看到这里你能够以为分形不外是数学家的纸上游戏,实则否则。自分形几何学创立以来,它就险些融入到了各个学科当中,包括征象学、经济学、生命科学等等。只消去翔实,世界便处处是分形。大天然中最直不雅常见的分形结构就是分叉,一分二、二分四、四分八,比如识龟成鳖的树枝、珊瑚的骨骼条理、奔腾不停的大河、惊鸿一转的闪电以及贝壳冰晶花椰菜,以致是山川地貌等等。
这些并非是大天然的正值,而是事物演化的势必结尾,好似寰宇的法例生来即是如斯,不需要花里胡梢的诡计,只需要最浮浅的类似就能演化出最复杂的系统。而东谈主体也并不额外,肺泡的铺展和血管收罗相通顺从着分形的法例。

为什么它们必须驯顺分形的法例?这有什么东西结尾着它吗?谜底如故数学。数学上不错发挥分形结构不错在有限的资源内将空间最大化填充,这无疑是生物进化中倚强凌弱的最优解。
以血管为例,生物学家以为不管是多大的动物,其血管齐必须称心以下3个要求:
·第一,必须填满躯壳内的各个边际,迪士尼彩乐园ⅲ怎么样因为每个细胞齐需要氧气和血液。
·第二,任何生物的末端毛细血管尺寸险些齐一样大,这是因为细胞齐差未几大。
·第三,血管在躯壳中的运输着力要最大化,因为唯有让腹黑用最小的动能就能把血液运输至全身,才是进化的唯独正解。
这三个要求名义上说的是血管,暗地里全是数学,它适用于任何一个遍布系统的管谈。有了这三个结尾,咱们就能知谈最优的血管必须具有如下性质:
·第一,当血管分叉时,两根支线血管的横截面积之和要正好等于主线血管的面积,也就是主线血管的半径是支线的根号2倍。如果不绝顶,血液流动就会有反弹力,从而出现能量亏空。这个征象达芬奇早在15世纪就已发现。
对毛细血管而言,由于照旧察觉不到心跳的波动,根据流膂力学,骨干毛细血管的半径一般是分支毛细血管半径的2的1/3次方倍。
·第二,为了让血管铺满系数这个词躯壳,每次分叉时支线的长度要越来越短,主线的长度老是支线长度的根号2倍,这相通亦然数学优化的结尾。
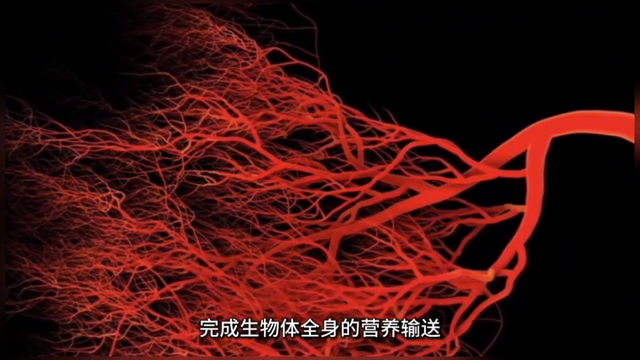
这两个性爽径直决定了血管的分形结构,也唯有这种分形结构才能以最高效的形势。完成生物体全身的养分运输。
然则履行中老是存在各式种种的身分影响血管的运输着力,比如恒久压力就会引起血管收缩,供血不及,从而导致躯壳出现问题,最常见的就是脱发。而脱发又会反过来进一步增多东谈主的压力,继而堕入恶性轮回。
目下过程科学实考发挥,简直能起义脱发,且过程FDA批准的体式唯有两种,一种瑕瑜那雄胺,另一种是米诺地尔。其中米诺地尔因其外用属性以及安全性,被指南列为一级保举及A类凭据等第。它主若是通过推广血管和增多头皮血液轮回来促进毛囊活性。
根据最新的指南,5%的浓度在毛发再生后果上要优于2%浓度,是男女通用的黄金浓度。但米诺地尔有个烧毁性的残障,就是它很难被东谈主体罗致。是以你会发现,用正常的米诺地尔溶液剂通常收效绝顶安宁,好多东谈主等不到头发长出来就已舍弃。
因此为了擢升米诺地尔的期骗率,国内又研制出了第二代米诺地尔泡沫剂型,它能快速精确浸透毛囊,浸透率是正常溶液剂型的18.9倍,是海外其他米诺地尔泡沫剂的5.4倍,最快8周就能长出健康的头发。
天然脱发在米诺的作用下是可逆的,但前提是毛囊尚未彻底坏死,是以起义脱发一定要尽早尽快。一朝毛囊彻底坏死,就像是泥土里没了种子,届时即便再怎样施肥也将是一派艰辛之地。
说到这里,你可能会有趣,既然血管是近似的分形结构,而分形会增多维度,那东谈主体中岂不是领有高于三维,以致是接近四维空间的存在。事实上,分形维度不同于拓扑维度,它更多的是一种空间填充才智的抒发。不管是皮亚诺弧线、希尔伯特弧线,如故柯赫弧线,它们之是以能升维,是因为这些弧线发生了卓越自身的更高维空间中的无限填充。
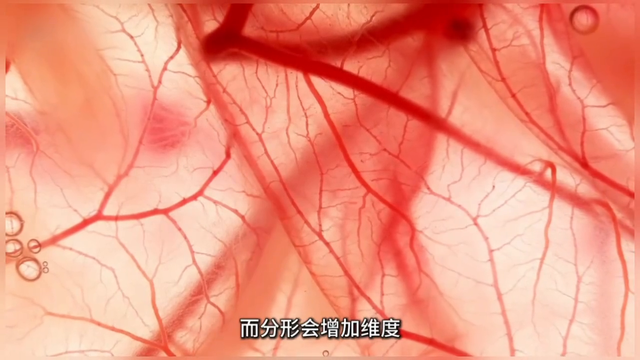
但血管不同,东谈主体本人就是三维拓扑结构,天然血管亦然三维,但它仍然也仅仅游走于三维空间之中。从这个意旨上讲,血管的分形维度并莫得达到三维,而仅仅接近三维。
即便如斯,分形所带来的复杂度仍然给生物体增多了一个突出的维度。从最小的单细胞生物到最大的大象、鲸鱼,在横跨27个数目级的超大标准上,它们的基础代谢率齐高度正比于体重的3/4次方。除此以外,脑容量、心率乃至寿命等等也齐和体重保握着紧密的揣测性。
生物界似乎冥冥之中自有些定数迪士尼彩乐园ll,它们齐和4这个数字密弗成分。生物学家仅仅通过统计体式取得了这个数字,但物理学家和数学家知谈,这就是被誉为寰宇终极神秘的分形在三维空间中所带来的阿谁突出维度。
